Differential Audio Inc.
Differential Audio Inc. was formed in the fall of 2022 after many years of working on a hobby project and is based in Ottawa, Ontario, Canada.
It is part of my mission to provide top class customer service, along with top class technology.
Part of my inspiration for this project has been my son, who was born with hearing loss. Following great support from CHEO (Children's Hospital of Eastern Ontario), we determined that his loss was due to a genetic deficiency affecting the hairs of his cochlea. This drove me forward to learn more about hearing, and with that synergy bring the additive synthesizer that I had dreamed of to market.
I hope you love it. Please contact me for any feedback you have.
Eric
About The Logo
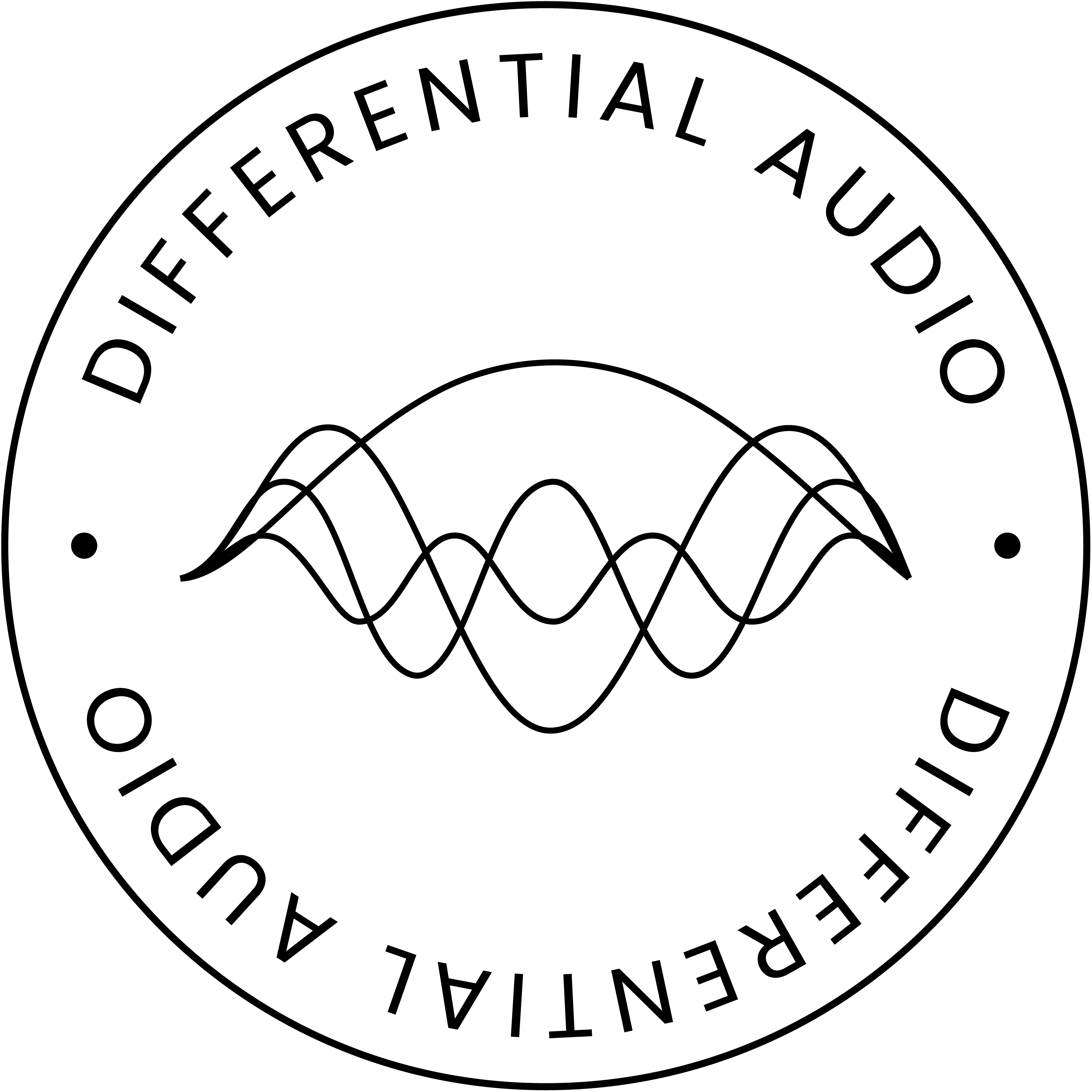
Please note that the waves described below that make up the Differential Audio Inc. logo are Registered in the U.S. Patent & Trademark Office.

This is a bit of a technical description of how I came up with the logo. Don't worry about it if you don't follow or aren't interested. You don't need to know any math to use the Eosynth.
The center of Differential Audio Inc.'s logo shows four different sine waves, at odd harmonics of the fundamental, listed below in order by their amplitudes from biggest to smallest. Each sine wave, or partial, is half a period short of a full sine wave, meaning it doesn't make a full rotation around back to its start in this view.
- The 1st sine wave has a period of 0.5 (1/2 cycles)
- The 2nd sine wave has a period of 1.5 (3/2 cycles)
- The 3rd, 2.5 (5/2 cycles)
- The 4th, 3.5 (7/2 cycles)
Time domain square waves, common in music synthesis, are defined by having odd frequency harmonics at integer multiples of (2*N + 1), where N=0 is the fundamental. So the 1st sine wave is the fundamental (1x), the 2nd is (2*1 + 1, or 3x) the fundamental, the 3rd is (2*2 + 1, or 5x), the 4th is (2*3 + 1, or 7x). Since the fundamental of the logo is only a half period (0.5), the 2nd, 3rd and 4th partials work out to be 1.5, 2.5 and 3.5 periods each.
Summing these four sine waves together forms the first four partials of a time domain square wave. A perfectly formed square wave will have an infinite amount of partials of decreasing amplitude.
https://en.wikipedia.org/wiki/Square_wave